Welcome to the world of calculus! This introduction provides a clear and accessible overview of calculus, perfect for beginners. Calculus For Dummies breaks down complex concepts into simple, understandable parts, making it easier to grasp the fundamentals. Whether you’re a student or just curious, this guide offers a friendly approach to learning calculus, connecting it to algebra and geometry for a solid foundation.
1.1 What is Calculus?
Calculus is a branch of mathematics that studies change and motion. It is divided into two main parts: differential calculus and integral calculus. Differential calculus deals with rates of change and slopes of curves, while integral calculus focuses on accumulation of quantities and areas under curves. Together, they provide powerful tools for solving problems in fields like physics, engineering, and economics. Calculus For Dummies simplifies these concepts, making them accessible to everyone. By breaking down complex ideas into manageable parts, it helps learners understand the fundamentals of calculus without getting overwhelmed.
1.2 Importance of Calculus in Real Life
Calculus plays a vital role in real-world applications, impacting various fields such as physics, engineering, economics, and biology. It helps in understanding rates of change, optimization, and accumulation, which are essential for solving practical problems. For instance, calculus is used in physics to calculate motion and forces, in engineering to design structures, and in economics to model market trends. Even in biology, it aids in studying population growth and disease spread. Calculus For Dummies highlights these applications, making the subject more relatable and demonstrating how it shapes everyday life and career opportunities.
Overview of Calculus 1
Calculus 1 introduces foundational concepts like limits, derivatives, and integrals. It builds a strong mathematical base, essential for understanding more complex topics in calculus. Topics include functions, continuity, and the Fundamental Theorem of Calculus, presented in an accessible way through examples and practical applications, as seen in Calculus For Dummies.
2.1 Structure and Topics Covered
Calculus 1 is structured to provide a comprehensive introduction to foundational concepts. Topics include limits, continuity, derivatives, and integrals, with a focus on practical applications. The course begins with an exploration of functions, their properties, and graphical interpretations, setting the stage for understanding rates of change and accumulation. Key concepts like the Power Rule, Product Rule, and Quotient Rule are introduced, alongside techniques for evaluating limits and solving optimization problems. The material is presented in a user-friendly manner, connecting calculus to algebra and geometry, ensuring a solid foundation for further study. This approach makes complex ideas accessible and engaging for newcomers to calculus.
2.2 Target Audience and Prerequisites
Calculus 1 for Dummies is designed for beginners, students, and anyone seeking to understand calculus without prior expertise. The target audience includes high school students, undergraduates, and individuals looking to refresh their math skills. No advanced mathematical knowledge is required, but a basic understanding of algebra and geometry is helpful. The book assumes familiarity with functions and graphs, though it reviews these concepts to ensure a solid foundation. It’s perfect for those who find math intimidating, offering a gentle, encouraging approach to learning calculus from the ground up.

Key Concepts in Calculus 1
Calculus 1 introduces limits, derivatives, and integrals, forming the foundation for understanding rates of change, optimization, and area under curves. These concepts are essential for further study.
3;1 Limits and Continuity
Limits and continuity are foundational concepts in calculus. A limit describes the behavior of a function as it approaches a specific point, while continuity ensures no breaks, jumps, or holes in the function. Understanding these ideas is crucial for analyzing function behavior and solving real-world problems. For instance, limits help determine the slope of a tangent line, and continuity ensures functions behave predictably. Calculus For Dummies provides concrete examples and exercises to master these concepts, making them accessible even for beginners. Practice these ideas thoroughly to build a strong calculus foundation.
3.2 Derivatives and Their Applications
Derivatives are a cornerstone of calculus, representing the rate at which a function changes. They are defined as the limit of the difference quotient and are governed by rules like the Power Rule. Applications of derivatives include finding slopes of tangent lines, optimizing functions, and solving related rates problems. Calculus For Dummies simplifies these concepts, offering step-by-step guidance and real-world examples. By mastering derivatives, you can analyze motion, economics, and engineering problems effectively. Regular practice and understanding these tools will enhance your problem-solving skills in various fields.
3.3 Integrals and Their Applications
Derivatives are a cornerstone of calculus, representing the rate at which a function changes. They are defined as the limit of the difference quotient and are governed by rules like the Power Rule. Applications of derivatives include finding slopes of tangent lines, optimizing functions, and solving related rates problems. Calculus For Dummies simplifies these concepts, offering step-by-step guidance and real-world examples. By mastering derivatives, you can analyze motion, economics, and engineering problems effectively. Regular practice and understanding these tools will enhance your problem-solving skills in various fields.
Learning Resources
Explore top resources like Calculus For Dummies and its workbook for clear explanations. Utilize online courses, tutorials, and study guides to enhance learning and problem-solving skills effectively.
4.1 Recommended Textbooks
Calculus For Dummies by Mark Ryan is a top choice for beginners. This user-friendly textbook explains complex concepts in simple terms, making calculus accessible to everyone. It emphasizes concrete examples before diving into formal formulas, ensuring a solid understanding of the basics. The book covers essential topics like limits, derivatives, and integrals, with practical problem-solving techniques. Available in hardcover, e-book, and PDF formats, it’s a versatile resource for self-study or classroom use. Pair it with the Calculus Workbook For Dummies for hands-on practice and reinforcement of key concepts.
4.2 Online Courses and Tutorials
Online courses and tutorials are excellent resources for mastering calculus. Platforms like Coursera and Khan Academy offer comprehensive courses tailored for beginners. These courses often include video lessons, interactive exercises, and quizzes to test your understanding. Additionally, official companion videos for Calculus For Dummies by Mark Ryan are available online, providing visual explanations of key concepts. Websites like Wolfram Alpha and Symbolab also offer step-by-step solutions to calculus problems, making them invaluable for practice and review. These tools complement the textbook and workbook, ensuring a well-rounded learning experience.
4.3 Study Guides and Workbooks
Study guides and workbooks are essential for reinforcing calculus concepts. Calculus For Dummies by Mark Ryan includes a companion workbook filled with practice problems and exercises. These resources provide hands-on experience, allowing you to apply theoretical knowledge to real-world scenarios. The workbook focuses on core topics like limits, derivatives, and integrals, with step-by-step solutions to help you understand common mistakes. Additionally, Calculus Workbook For Dummies offers over 1,000 practice problems, making it a valuable supplement to online courses and textbooks. These tools ensure you grasp the fundamentals and build confidence in your problem-solving skills.
Understanding Limits
Limits are the foundation of calculus, representing the value a function approaches as it nears a certain point. Calculus For Dummies explains this concept intuitively, connecting it to broader calculus principles like continuity and derivatives, ensuring a solid understanding of how functions behave.
5.1 Definition and Intuition
Limits form the cornerstone of calculus, defining the behavior of functions as they approach specific points. Intuitively, a limit represents the value a function aims for, even if it never actually reaches it. Calculus For Dummies simplifies this concept, explaining how limits help understand continuity and rates of change. By focusing on real-world examples, the book makes abstract ideas tangible, ensuring readers grasp the essence of limits before diving into derivatives and integrals. This foundational understanding is crucial for mastering more complex calculus topics later on.
5.2 Techniques for Evaluating Limits
Evaluating limits involves several key techniques to determine the behavior of functions. Direct substitution is the simplest method when possible. Factoring and canceling common terms help simplify expressions. For indeterminate forms like 0/0, conjugate multiplication or using L’Hôpital’s Rule is effective. Numerical evaluation and graphical analysis provide approximations. Calculus For Dummies offers clear examples and step-by-step guidance, ensuring readers master these methods intuitively. These techniques are essential for understanding continuity and rates of change, forming a solid foundation for advanced calculus concepts.
Derivatives
Derivatives measure rates of change and function slopes. Key rules include the Power, Product, Quotient, and Chain Rules, essential for calculus problem-solving.
6.1 Definition and Rules
A derivative measures the rate at which a function changes, representing the slope of the tangent line at any point. The Power Rule states that the derivative of ( x^n ) is ( nx^{n-1} ). The Product Rule and Quotient Rule handle multiplication and division of functions, respectively. The Chain Rule applies to composite functions. For example, the derivative of ( x^2 ) is ( 2x ). These rules are foundational for solving calculus problems, providing tools to analyze and simplify complex functions effectively.
6.2 Applications in Optimization
Derivatives are essential for optimizing functions, whether maximizing profit or minimizing cost. By finding where the derivative is zero or undefined, you identify critical points. These points help determine maxima, minima, or saddle points. In business, calculus optimizes resource allocation and pricing strategies. In physics, it finds equilibrium points. For example, a company might use derivatives to find the price that maximizes revenue. By analyzing the first and second derivatives, you can confirm if a critical point is a maximum or minimum. This practical application of calculus is crucial for solving real-world problems efficiently.

Integrals
Integrals represent the accumulation of quantities and are the reverse process of derivatives. They are used to find the area under curves and solve problems involving accumulation.
7.1 Definite and Indefinite Integrals
Definite integrals calculate the net area between a function and the x-axis within specific bounds, yielding a numerical result. Indefinite integrals, however, represent the family of functions whose derivatives are the original function, involving a constant of integration. Both concepts are foundational in calculus, enabling problem-solving in various fields like physics and engineering. Calculus For Dummies provides clear examples and step-by-step explanations to master these integral types, ensuring a comprehensive understanding of their applications and computations.
7;2 Techniques of Integration
Mastering integration techniques is essential for solving complex calculus problems. Common methods include substitution, integration by parts, and partial fractions. Substitution simplifies integrals by changing variables, while integration by parts applies when integrating products of functions. Partial fractions break down rational functions into simpler terms. These techniques, along with power rule and trigonometric integrals, are thoroughly explained in Calculus For Dummies, providing clear examples and practice exercises. Understanding these methods allows you to tackle a wide range of integrals, from basic to advanced, with confidence and accuracy.
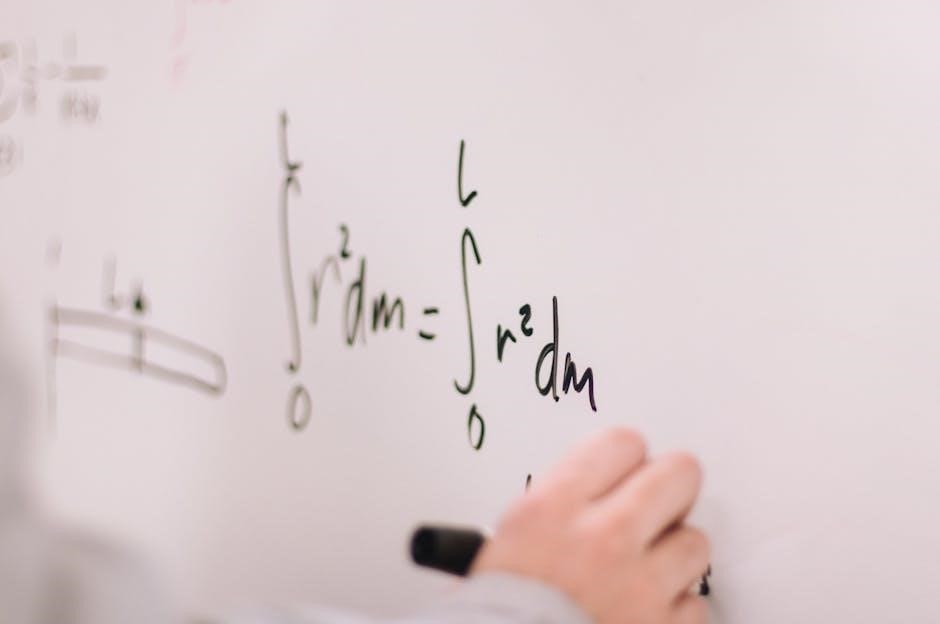
Applications of Calculus
Calculus has vast real-world applications in physics, engineering, economics, and biology. It helps model change, optimize systems, and understand rates of change and accumulation, making it indispensable in these fields.
8.1 Physics and Engineering
In physics and engineering, calculus is essential for describing motion, forces, and energy. It helps model real-world phenomena like acceleration, velocity, and electromagnetism. Engineers use calculus to design structures, optimize systems, and analyze signals. For instance, differential equations, derived from calculus, are crucial in understanding wave patterns and heat transfer. Calculus For Dummies provides practical examples, such as calculating distances traveled by objects under constant acceleration, making complex concepts accessible. This foundational knowledge enables professionals to solve practical problems and innovate in their fields effectively.
8.2 Economics and Biology
Calculus plays a vital role in economics and biology, offering tools to model and analyze dynamic systems. In economics, it helps determine optimal prices, maximize profits, and understand market trends through concepts like supply and demand. Marginal analysis, a key calculus application, evaluates how small changes affect outcomes. In biology, calculus models population growth, disease spread, and ecosystems. It also aids in understanding metabolic rates and biological processes. Calculus For Dummies provides clear examples, such as calculating economic equilibrium and modeling exponential growth in populations, making these concepts accessible and practical for learners.
Study Tips and Tricks
Master calculus by understanding core concepts, practicing regularly, and breaking problems into smaller steps. Use visualization tools and seek help when stuck. Calculus For Dummies offers clear guidance and practical examples to simplify learning.
9.1 Effective Study Habits
Developing strong study habits is crucial for mastering calculus. Start by breaking problems into smaller, manageable parts and solving them step-by-step. Regular practice helps build familiarity with concepts. Use visualization tools like graphs to understand complex ideas. Set specific goals for each study session and review notes daily. Calculus For Dummies recommends focusing on understanding rather than memorizing formulas. Engage with examples, ask questions, and seek help when needed. Consistency and patience are key to overcoming challenges in calculus.
9.2 Common Mistakes to Avoid
When learning calculus, avoid common pitfalls that can hinder progress. Misunderstanding limit properties and incorrectly applying derivative rules are frequent errors. Forgetting to check intervals when dealing with increasing/decreasing functions can lead to inaccurate conclusions. Another mistake is mishandling integral techniques, such as improper substitution or ignoring constants. Poor algebraic manipulation, like incorrect factoring, can compound problems. Neglecting to verify solutions, especially after applying optimization techniques, is also a oversight. To avoid these errors, carefully review each step, practice regularly, and seek clarification when unsure. Calculus For Dummies emphasizes the importance of meticulous problem-solving habits.
Technology and Tools
Utilize graphing calculators for visualizing functions and solving equations. Calculus software like Desmos and Wolfram Alpha aids in computations and understanding complex concepts. These tools enhance problem-solving efficiency.
10.1 Graphing Calculators
Graphing calculators are essential tools for mastering calculus concepts. They allow students to visualize functions, derivatives, and integrals, making complex ideas more tangible. Popular models like the TI-84 and Casio Prizm simplify tasks such as limit evaluations, numerical integration, and function analysis. These calculators also support advanced features like parametric graphing and 3D plotting, which are useful for understanding multivariable calculus. By leveraging graphing calculators, students can explore mathematical relationships dynamically, enhancing their problem-solving skills and intuition. They are invaluable companions for both classroom learning and independent study, bridging the gap between theory and practical application.
10.2 Calculus Software
Calculus software provides powerful tools for solving complex mathematical problems and visualizing concepts. Programs like Wolfram Alpha, GeoGebra, and Maple offer advanced features such as symbolic computation, graphing, and step-by-step solutions. These tools are ideal for understanding derivatives, integrals, and differential equations. They also support interactive simulations, enabling users to explore calculus principles dynamically. For learners, calculus software enhances problem-solving skills and provides a deeper understanding of mathematical relationships. Many platforms offer free or student versions, making them accessible for educational use. These resources complement traditional study methods, offering a modern approach to mastering calculus concepts.
Exam Preparation
Effective exam preparation involves using Calculus For Dummies study guides and workbooks to practice problems and review key concepts. Regularly solving past papers enhances problem-solving skills and time management.
11.1 Strategies and Tips
Mastering calculus requires effective study strategies. Start by understanding key concepts thoroughly before moving to advanced topics. Utilize study guides like Calculus For Dummies and workbooks for practice problems. Solve past exam papers to improve problem-solving skills and time management. Focus on understanding rather than memorizing formulas. Highlight important equations and theorems for quick review. Practice regularly to build confidence. Review mistakes to avoid repetition. Seek help when stuck to ensure clarity. By following these tips, you’ll approach exams with confidence and achieve success in calculus.
11.2 Review Materials and Practice Exams
Enhance your exam preparation with comprehensive review materials and practice exams. Utilize resources like Calculus For Dummies and its companion workbook for targeted practice problems. Past exam papers provide valuable insights into question formats and difficulty levels. Regularly solving practice exams helps improve time management and reduces exam anxiety; Focus on understanding mistakes to avoid repeating them. Use study guides to review key concepts and formulas. Simulate exam conditions during practice to build confidence. These materials ensure a well-rounded preparation, helping you approach calculus exams with clarity and assurance.

Advanced Topics in Calculus 1
Explore advanced topics like optimization, related rates, and an introduction to differential equations. These concepts build on foundational calculus principles, enhancing problem-solving skills and real-world applications.
12.1 Optimization and Related Rates
Optimization and related rates are advanced topics in Calculus 1 that involve finding maxima, minima, or related changes in rates. Optimization problems require identifying the best possible solution within constraints, often using derivatives. Related rates problems involve differentiating with respect to time, applying the chain rule to relate variables. These concepts are crucial in physics, engineering, and economics. Calculus For Dummies simplifies these ideas with concrete examples, making them accessible for beginners. By mastering these techniques, students can solve real-world problems efficiently, enhancing their analytical and problem-solving skills.
Differential equations are equations involving an unknown function and its derivatives. They are fundamental in modeling dynamic systems, such as population growth or heat transfer. In Calculus 1, the focus is on basic concepts, such as first-order equations and separation of variables. Calculus For Dummies provides a gentle introduction, emphasizing intuitive understanding over advanced techniques. These equations are essential in physics, engineering, and biology, allowing students to describe and predict system behaviors. This section lays the groundwork for deeper exploration in higher-level calculus courses, ensuring a solid foundation for problem-solving in real-world scenarios.
Importance of Practice
Regular practice is essential for mastering calculus concepts. It enhances problem-solving skills and builds confidence. Resources like workbooks and past exams are key to consistent improvement and understanding.
13.1 Regular Problem Solving
Regular problem solving is a cornerstone of mastering calculus. It helps reinforce concepts, improves analytical skills, and builds confidence. Calculus For Dummies and its workbook provide numerous exercises to practice limits, derivatives, and integrals. Consistent practice ensures a deeper understanding of fundamental principles. By solving problems regularly, students can identify weak areas and improve their ability to apply calculus to real-world scenarios. This habit also enhances critical thinking and prepares learners for more complex topics in subsequent courses. Regular problem solving is essential for long-term success in calculus and its applications.
13.2 Past Exam Papers
Reviewing past exam papers is a powerful study strategy for calculus students. It provides insights into common question types and exam formats. Calculus For Dummies and related resources often include practice exams that simulate real test conditions. Solving these papers helps improve time management and reduces anxiety. By identifying recurring themes and challenging areas, students can focus their study efforts effectively. Past exams also serve as valuable tools for self-assessment, allowing learners to gauge their progress and readiness for actual tests. Regular practice with past papers enhances problem-solving skills and boosts confidence in tackling calculus exams successfully.
Mastering Calculus 1 sets a strong foundation for advanced topics. Use resources like Calculus 1 For Dummies PDF to reinforce learning. Regular practice and review ensure long-term understanding and prepare you for Calculus 2.
14.1 Summary of Key Takeaways
Calculus 1 For Dummies PDF provides a comprehensive guide for beginners, covering foundational concepts like limits, derivatives, and integrals. It emphasizes practical applications and real-world examples, making complex ideas accessible. The book connects calculus to algebra and geometry, ensuring a solid understanding. Key takeaways include mastering techniques for evaluating limits, applying derivatives for optimization, and solving integrals for area calculations. Regular practice and review are stressed as essential for success. This resource is ideal for students seeking a clear, user-friendly approach to grasp calculus fundamentals and prepare for advanced topics like Calculus 2.
14.2 Preparing for Calculus 2
Mastering Calculus 1 is essential for a smooth transition to Calculus 2. Focus on understanding limits, derivatives, and integrals deeply, as these concepts form the backbone of advanced topics. Practice problem-solving regularly to strengthen your foundation. Review key applications like optimization and related rates, which are crucial for more complex calculations. Ensure proficiency in techniques of integration and differential equations, as they are central to Calculus 2. Utilize resources like Calculus For Dummies and practice workbooks to reinforce learning. Building a strong grasp of Calculus 1 concepts will pave the way for success in the next level of your studies.
