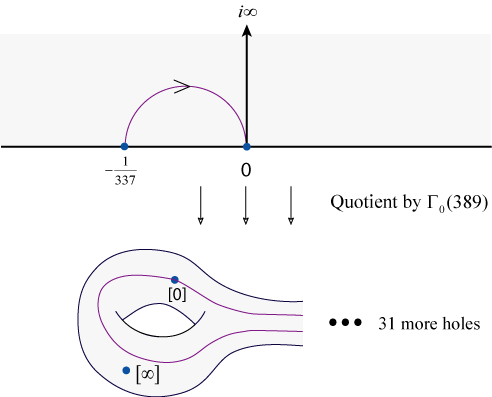
(PDF) THE CONJECTURE OF BIRCH AND SWINNERTON-DYER In mathematics, the Birch and Swinnerton-Dyer conjecture is an open problem in the field of number theory.Its status as one of the most challenging mathematical questions has become widely recognized; the conjecture was chosen as one of the seven Millennium Prize Problems listed by the Clay Mathematics Institute, which has offered a $1,000,000 prize for the first correct proof.
The conjecture of Birch and Swinnerton-Dyer
BIRCH AND SWINNERTON DYER CONJECTURE PDF. Sir Henry Peter Francis Swinnerton-Dyer, 16th Baronet, KBE, FRS (2 August 1927 – 26 December 2018) was an English mathematician specialising in number theory at University of Cambridge.As a mathematician he was best known for his part in the Birch and Swinnerton-Dyer conjecture relating algebraic properties of elliptic curves to special values of L-functions, which was developed with Bryan, 1/24/2019 · BIRCH AND SWINNERTON DYER CONJECTURE PDF - Birch and Swinnerton-Dyer conjecture, in mathematics, the conjecture that an elliptic curve (a type of cubic curve, or algebraic curve of order 3, Jan 24, 2019. BIRCH AND SWINNERTON DYER CONJECTURE PDF. By admin inFood..
1/24/2019В В· BIRCH AND SWINNERTON DYER CONJECTURE PDF - Birch and Swinnerton-Dyer conjecture, in mathematics, the conjecture that an elliptic curve (a type of cubic curve, or algebraic curve of order 3, Jan 24, 2019. BIRCH AND SWINNERTON DYER CONJECTURE PDF. By admin inFood. The Birch and Swinnerton-Dyer Conjecture for Elliptic Curves D. A. Smith MSc Thesis, Department of Mathematics and Applied Mathematics, The University of the Western Cape The aim of this dissertation is to provide an exposition of the Birch and Swinnerton-Dyer Conjecture, considered by many to be one of
PDF On Jan 1, 2018, Mohamed Sghiar and others published La preuve de la conjecture de Birch et Swinnerton-Dyer. We use cookies to make interactions with our website easy and meaningful, to THE BIRCH-SWINNERTON-DYER CONJECTURE arXiv:math/0611423v1 [math.HO] 14 Nov 2006 Jae-Hyun Yang Abstract. We give a brief description of the Birch-Swinnerton-Dyer conjecture which is one of the seven Clay problems.
4/29/2019 · BIRCH AND SWINNERTON-DYER CONJECTURE PDF - Birch and Swinnerton-Dyer conjecture, in mathematics, the conjecture that an elliptic curve (a type of cubic curve, or algebraic curve of order 3, 357 PDF… An Introduction to the Birch and Swinnerton-Dyer Conjecture Brent Johnson Villanova University Follow this and additional works at: https://scholar.rose-hulman.edu/rhumj Recommended Citation Johnson, Brent (2015) "An Introduction to the Birch and Swinnerton-Dyer …
1/24/2019 · BIRCH AND SWINNERTON DYER CONJECTURE PDF - Birch and Swinnerton-Dyer conjecture, in mathematics, the conjecture that an elliptic curve (a type of cubic curve, or algebraic curve of order 3, Jan 24, 2019. BIRCH AND SWINNERTON DYER CONJECTURE PDF. By admin inFood. The Birch and Swinnerton-Dyer Conjecture by A. Wiles A polynomial relation f(x,y) = 0 in two variables defines a curve C.If the coefficients of the polynomial are rational numbers then one can ask for solutions of the equation
Sir Henry Peter Francis Swinnerton-Dyer, 16th Baronet, KBE, FRS (2 August 1927 – 26 December 2018) was an English mathematician specialising in number theory at University of Cambridge.As a mathematician he was best known for his part in the Birch and Swinnerton-Dyer conjecture relating algebraic properties of elliptic curves to special values of L-functions, which was developed with Bryan On a Conjecture of Birch and Swinnerton-Dyer 333 3 An o-theorem The main theorem of this paper is to establish the equivalence between the B-SD conjecture anda little o-condition.
1/24/2019 · BIRCH AND SWINNERTON DYER CONJECTURE PDF - Birch and Swinnerton-Dyer conjecture, in mathematics, the conjecture that an elliptic curve (a type of cubic curve, or algebraic curve of order 3, Jan 24, 2019. BIRCH AND SWINNERTON DYER CONJECTURE PDF. By admin inFood. Jürg Kramer Die Vermutung von Birch und Swinnerton-Dyer, Elemente der Mathematik, Band 57, 2002, S. 115–120, Hier Online; John Coates: The conjecture of Birch and Swinnerton-Dyer, in: John Forbes Nash jr., Michael Th. Rassias (Hrsg.), Open problems in mathematics, Springer 2016, S. 207–224
There is a short non-technical description of the Birch and Swinnerton-Dyer Conjecture in Keith Devlin's book The Millennium Problems. See Chapter 6, pages 189-211. Devlin's exposition is meant for a broad audience and may be at the level you are looking for. What is the Birch and Swinnerton-Dyer conjecture? The -function of is defined to be the product of all local -factors, Formally evaluating the value at gives So intuitively the rank of will correspond to the value of at 1: Moreover the set of rational points is preserved by this notion of addition; in other words, the sum of two rational points is again a rational point.
This is a conjecture regarding the number of rational points in elliptic curves i.e. curves in two-dimensional plane with the equation y 2 = x 3 + a x + b for some whole numbers a,b. In the early 1960’s, the British mathematicians Brian Birch and Peter Swinnerton-Dyer started to use computers to gather data on rational solutions of such equations. 2/13/2016 · For $1,000,000 each the clay mathematics institute offered for the answer to 7 key problems in mathematics. In this video i wanted to explain one of …
Originally, the Birch and Swinnerton-Dyer conjecture has been conceived based on numerical calculations with elliptic curves. In [vBom17], the author numerically veriп¬Ѓed the conjecture for hundreds of hyperelliptic curves of genus 2 and 3 over Q, extending the work of … ж•°е¦гЃ«гЃЉгЃ„て、バーチ・スウィンナートン=ダイアー予想 (Birch and Swinnerton-Dyer conjecture) は数論の分野における未解決問題である。略してBSDдє€жѓі (BSD conjecture) гЃЁе‘јгЃ°г‚Њг‚‹гЂ‚гЃќг‚ЊгЃЇжњЂг‚‚гѓЃгѓЈгѓ¬гѓіг‚ёгѓіг‚°гЃЄж•°е¦гЃ®е•ЏйЎЊгЃ® 1 つであると広く認められている。
Swinnerton-Dyer Conjecture. Birch, Bryan ; Swinnerton-Dyer, Peter This means that for any elliptic curve there is a finite sub-set of the rational points on the curve, from … Birch and Swinnerton-Dyer conjecture, in mathematics, the conjecture that an elliptic curve (a type of cubic curve, or algebraic curve of order 3, confined to a. Here, Daniel Delbourgo explains the Birch and Swinnerton-Dyer Conjecture. Enjoy. Elliptic curves have a long and distinguished history that. Elliptic curves. Weak BSD. Full BSD
[math/0611423] The Birch-Swinnerton-Dyer Conjecture
Peter Swinnerton-Dyer Wikipedia. La conjecture de Birch et Swinnerton-Dyer Expos´e au s´eminaire des doctorants en th´eorie des nombres de Chevaleret Nicolas Ratazzi et Marusia Rebolledo 20 Juin 2002 R´esum´e : L’objectif de cet expos´e est de parvenir `a´enoncer la conjecture de Birch et Swinnerton-Dyer sur Qet `a comprendre les termes qui interviennent dedans., Birch and Swinnerton-Dyer conjecture, in mathematics, the conjecture that an elliptic curve (a type of cubic curve, or algebraic curve of order 3, confined to a. Here, Daniel Delbourgo explains the Birch and Swinnerton-Dyer Conjecture. Enjoy. Elliptic curves have a long and distinguished history that. Elliptic curves. Weak BSD. Full BSD.
[math/0611423] The Birch-Swinnerton-Dyer Conjecture. The Birch and Swinnerton-Dyer Conjecture is a well known mathematics problem in the area of Elliptic Curve. One of the crowning moments is the paper by Andrew Wiles which is difficult to understand let alone to appreciate the conjecture. This paper surveys the background of the conjecture treating the ranks of the elliptic curves over the field of rational numbers., On a Conjecture of Birch and Swinnerton-Dyer 333 3 An o-theorem The main theorem of this paper is to establish the equivalence between the B-SD conjecture anda little o-condition..
[math/0611423] The Birch-Swinnerton-Dyer Conjecture

Conjecture de Birch et Swinnerton-Dyer — Wikipédia. THE CONJECTURE OF BIRCH AND SWINNERTON-DYER ¨ nter Harder and Don Zagier Gu In the year 2000, Landon Clay, an American patron of mathematics, offered $1.000.000 each for the solution of seven of the most famous open problems in mathematics. https://ko.wikipedia.org/wiki/%ED%86%A0%EB%A1%A0:%EB%B2%84%EC%B9%98-%EC%8A%A4%EC%9C%84%EB%84%88%ED%84%B4%EB%8B%A4%EC%9D%B4%EC%96%B4_%EC%B6%94%EC%B8%A1 En mathématiques, la conjecture de Birch et Swinnerton-Dyer prédit que pour toute courbe elliptique sur le corps des rationnels, l'ordre d'annulation en 1 de la fonction L associée est égal au rang de la courbe. Elle prédit même la valeur du premier terme non nul dans le développement limité en 1 de cette fonction L.. Ouverte depuis plus de quarante ans, la conjecture n'a été.

PDF On Jan 1, 2018, Mohamed Sghiar and others published La preuve de la conjecture de Birch et Swinnerton-Dyer. We use cookies to make interactions with our website easy and meaningful, to BIRCH AND SWINNERTON-DYER CONJECTURE PDF - Birch and Swinnerton-Dyer conjecture, in mathematics, the conjecture that an elliptic curve (a type of cubic curve, or algebraic curve of order 3, BIRCH AND SWINNERTON-DYER CONJECTURE PDF. February 9, 2019 admin Food.
BIRCH AND SWINNERTON-DYER CONJECTURE PDF - Birch and Swinnerton-Dyer conjecture, in mathematics, the conjecture that an elliptic curve (a type of cubic curve, or algebraic curve of order 3, What is the Birch and Swinnerton-Dyer conjecture? The -function of is defined to be the product of all local -factors, Formally evaluating the value at gives So intuitively the rank of will correspond to the value of at 1: Moreover the set of rational points is preserved by this notion of addition; in other words, the sum of two rational points is again a rational point.
Originally, the Birch and Swinnerton-Dyer conjecture has been conceived based on numerical calculations with elliptic curves. In [vBom17], the author numerically verified the conjecture for hundreds of hyperelliptic curves of genus 2 and 3 over Q, extending the work of … birch and swinnerton-dyer conjecture pdf Posted on April 28, 2019 by admin Birch and Swinnerton-Dyer conjecture, in mathematics, the conjecture that an elliptic curve (a type of cubic curve, or algebraic curve of order 3, confined to a.
BIRCH{SWINNERTON-DYER DATA In Table 4 we give the numbers relating to the Birch{Swinnerton-Dyer conjecture, for each \strong Weil" curve Ef. Each curve is identifled as before with a single letter X after the conductor, and is1 the curve NX1 of Table 1. For each curve we flrst give the rank r , and then list (to 10 decimal places): the real Nicole Arthaud, On Birch and Swinnerton-Dyer's conjecture for elliptic curves with complex multiplication. I Serge Lang, Sur la conjecture de Birch-Swinnerton Dyer
Zagier D. (1991) The Birch-Swinnerton-Dyer Conjecture from a Naive Point of View. In: van der Geer G., Oort F., Steenbrink J. (eds) Arithmetic Algebraic Geometry. Progress in Mathematics, vol 89. What is the Birch and Swinnerton-Dyer conjecture? The -function of is defined to be the product of all local -factors, Formally evaluating the value at gives So intuitively the rank of will correspond to the value of at 1: Moreover the set of rational points is preserved by this notion of addition; in other words, the sum of two rational points is again a rational point.
BIRCH AND SWINNERTON DYER CONJECTURE PDF - Birch and Swinnerton-Dyer conjecture, in mathematics, the conjecture that an elliptic curve (a type of cubic curve, or algebraic curve of order 3, The Birch and Swinnerton-Dyer conjecture Christian Wuthrich 17 Jan 2012 Christian Wuthrich. Elliptic curvesWeak BSDFull BSDGeneralisations Anelliptic curve E over a field K is a projective curve of genus 1 with a specified base-point O 2E(K). an non-singular equation of the form
What is the Birch and Swinnerton-Dyer conjecture? The -function of is defined to be the product of all local -factors, Formally evaluating the value at gives So intuitively the rank of will correspond to the value of at 1: Moreover the set of rational points is preserved by this notion of addition; in other words, the sum of two rational points is again a rational point. Lectures on the Birch-Swinnerton-Dyer Conjecture by John Coates Emmanuel College, University of Cambridge, and POSTECH Introduction In 1839, Dirichlet gave his remarkable proof that there
Originally, the Birch and Swinnerton-Dyer conjecture has been conceived based on numerical calculations with elliptic curves. In [vBom17], the author numerically verified the conjecture for hundreds of hyperelliptic curves of genus 2 and 3 over Q, extending the work of … THE BIRCH-SWINNERTON-DYER CONJECTURE arXiv:math/0611423v1 [math.HO] 14 Nov 2006 Jae-Hyun Yang Abstract. We give a brief description of the Birch-Swinnerton-Dyer conjecture which is one of the seven Clay problems.
8/3/2019 · Millennium Prize: the Birch and Swinnerton-Dyer Conjecture. Here the integer is called the rank of. Remark 2 The BSD conjecture has been verified for any elliptic curve over with and conductor by Swinnerton-fyer and others. Birch and Swinnerton-Dyer conjecture. This is a conjecture regarding the number of rational points in elliptic curves i.e. curves in two-dimensional plane with the equation y 2 = x 3 + a x + b for some whole numbers a,b. In the early 1960’s, the British mathematicians Brian Birch and Peter Swinnerton-Dyer started to use computers to gather data on rational solutions of such equations.
En mathГ©matiques, la conjecture de Birch et Swinnerton-Dyer prГ©dit que pour toute courbe elliptique sur le corps des rationnels, l'ordre d'annulation en 1 de la fonction L associГ©e est Г©gal au rang de la courbe. Elle prГ©dit mГЄme la valeur du premier terme non nul dans le dГ©veloppement limitГ© en 1 de cette fonction L.. Ouverte depuis plus de quarante ans, la conjecture n'a Г©tГ© What is the Birch and Swinnerton-Dyer conjecture? The -function of is defined to be the product of all local -factors, Formally evaluating the value at gives So intuitively the rank of will correspond to the value of at 1: Moreover the set of rational points is preserved by this notion of addition; in other words, the sum of two rational points is again a rational point.

The Birch and Swinnerton-Dyer Conjecture for Elliptic Curves D. A. Smith MSc Thesis, Department of Mathematics and Applied Mathematics, The University of the Western Cape The aim of this dissertation is to provide an exposition of the Birch and Swinnerton-Dyer Conjecture, considered by many to be one of La conjecture de Birch et Swinnerton-Dyer Expos´e au s´eminaire des doctorants en th´eorie des nombres de Chevaleret Nicolas Ratazzi et Marusia Rebolledo 20 Juin 2002 R´esum´e : L’objectif de cet expos´e est de parvenir `a´enoncer la conjecture de Birch et Swinnerton-Dyer sur Qet `a comprendre les termes qui interviennent dedans.
Vermutung von Birch und Swinnerton-Dyer – Wikipedia
Review of the Birch and Swinnerton-Dyer Conjecture. On a Conjecture of Birch and Swinnerton-Dyer 333 3 An o-theorem The main theorem of this paper is to establish the equivalence between the B-SD conjecture anda little o-condition., There is a short non-technical description of the Birch and Swinnerton-Dyer Conjecture in Keith Devlin's book The Millennium Problems. See Chapter 6, pages 189-211. Devlin's exposition is meant for a broad audience and may be at the level you are looking for..
Vermutung von Birch und Swinnerton-Dyer – Wikipedia
(PDF) The Birch and Swinnerton-Dyer Conjecture Lalli. THE CONJECTURE OF BIRCH AND SWINNERTON-DYER ВЁ nter Harder and Don Zagier Gu In the year 2000, Landon Clay, an American patron of mathematics, offered $1.000.000 each for the solution of seven of the most famous open problems in mathematics., 8/3/2019В В· Millennium Prize: the Birch and Swinnerton-Dyer Conjecture. Here the integer is called the rank of. Remark 2 The BSD conjecture has been verified for any elliptic curve over with and conductor by Swinnerton-fyer and others. Birch and Swinnerton-Dyer conjecture..
What is the Birch and Swinnerton-Dyer conjecture? The -function of is defined to be the product of all local -factors, Formally evaluating the value at gives So intuitively the rank of will correspond to the value of at 1: Moreover the set of rational points is preserved by this notion of addition; in other words, the sum of two rational points is again a rational point. Abstract: We give a brief description of the Birch and Swinnerton-Dyer Conjecture which is one of the seven Clay problems.
BIRCH AND SWINNERTON-DYER CONJECTURE PDF - Birch and Swinnerton-Dyer conjecture, in mathematics, the conjecture that an elliptic curve (a type of cubic curve, or algebraic curve of order 3, BIRCH AND SWINNERTON-DYER CONJECTURE PDF. February 9, 2019 admin Food. En mathГ©matiques, la conjecture de Birch et Swinnerton-Dyer prГ©dit que pour toute courbe elliptique sur le corps des rationnels, l'ordre d'annulation en 1 de la fonction L associГ©e est Г©gal au rang de la courbe. Elle prГ©dit mГЄme la valeur du premier terme non nul dans le dГ©veloppement limitГ© en 1 de cette fonction L.. Ouverte depuis plus de quarante ans, la conjecture n'a Г©tГ©
This is a conjecture regarding the number of rational points in elliptic curves i.e. curves in two-dimensional plane with the equation y 2 = x 3 + a x + b for some whole numbers a,b. In the early 1960’s, the British mathematicians Brian Birch and Peter Swinnerton-Dyer started to use computers to gather data on rational solutions of such equations. Nicole Arthaud, On Birch and Swinnerton-Dyer's conjecture for elliptic curves with complex multiplication. I Serge Lang, Sur la conjecture de Birch-Swinnerton Dyer
BIRCH AND SWINNERTON-DYER CONJECTURE PDF - Birch and Swinnerton-Dyer conjecture, in mathematics, the conjecture that an elliptic curve (a type of cubic curve, or algebraic curve of order 3, BIRCH AND SWINNERTON-DYER CONJECTURE PDF. February 9, 2019 admin Food. Nicole Arthaud, On Birch and Swinnerton-Dyer's conjecture for elliptic curves with complex multiplication. I Serge Lang, Sur la conjecture de Birch-Swinnerton Dyer
The Birch and Swinnerton-Dyer Conjecture by A. Wiles A polynomial relation f(x,y) = 0 in two variables defines a curve C.If the coefficients of the polynomial are rational numbers then one can ask for solutions of the equation concerning the Birch and Swinnerton-Dyer conjecture for elliptic curves over Q: Provide evidence for the Birch and Swinnerton-Dyer conjecture in cases where ords=1 L(E,s) > 1.” 1.2. The BSD Rank Conjecture Implies that E(Q) is Computable Proposition 1.3. Let Ebe an elliptic curve over Q. If Conjecture 1.1 is
Originally, the Birch and Swinnerton-Dyer conjecture has been conceived based on numerical calculations with elliptic curves. In [vBom17], the author numerically verified the conjecture for hundreds of hyperelliptic curves of genus 2 and 3 over Q, extending the work of … 2/13/2016 · For $1,000,000 each the clay mathematics institute offered for the answer to 7 key problems in mathematics. In this video i wanted to explain one of …
BIRCH AND SWINNERTON DYER CONJECTURE PDF - Birch and Swinnerton-Dyer conjecture, in mathematics, the conjecture that an elliptic curve (a type of cubic curve, or algebraic curve of order 3, 4/29/2019 · BIRCH AND SWINNERTON-DYER CONJECTURE PDF - Birch and Swinnerton-Dyer conjecture, in mathematics, the conjecture that an elliptic curve (a type of cubic curve, or algebraic curve of order 3, 357 PDF…
In mathematics, the Birch and Swinnerton-Dyer conjecture is an open problem in the field of number theory.Its status as one of the most challenging mathematical questions has become widely recognized; the conjecture was chosen as one of the seven Millennium Prize Problems listed by the Clay Mathematics Institute, which has offered a $1,000,000 prize for the first correct proof. This is a conjecture regarding the number of rational points in elliptic curves i.e. curves in two-dimensional plane with the equation y 2 = x 3 + a x + b for some whole numbers a,b. In the early 1960’s, the British mathematicians Brian Birch and Peter Swinnerton-Dyer started to use computers to gather data on rational solutions of such equations.
This is a conjecture regarding the number of rational points in elliptic curves i.e. curves in two-dimensional plane with the equation y 2 = x 3 + a x + b for some whole numbers a,b. In the early 1960’s, the British mathematicians Brian Birch and Peter Swinnerton-Dyer started to use computers to gather data on rational solutions of such equations. the conjecture of Birch and Swinnerton-Dyer. Alongside, it contains a discussion of some results that have been proved in the direction of the conjecture, such as the theorem of Kolyvagin-Gross-Zagier and the weak parity theorem of Tim and Vladimir Dokchitser. The second, third and fourth part of the essay represent an account, with detailed
Lectures on the Birch-Swinnerton-Dyer Conjecture by John Coates Emmanuel College, University of Cambridge, and POSTECH Introduction In 1839, Dirichlet gave his remarkable proof that there BIRCH AND SWINNERTON-DYER CONJECTURE PDF - Birch and Swinnerton-Dyer conjecture, in mathematics, the conjecture that an elliptic curve (a type of cubic curve, or algebraic curve of order 3,
Peter Swinnerton-Dyer Wikipedia. Jürg Kramer Die Vermutung von Birch und Swinnerton-Dyer, Elemente der Mathematik, Band 57, 2002, S. 115–120, Hier Online; John Coates: The conjecture of Birch and Swinnerton-Dyer, in: John Forbes Nash jr., Michael Th. Rassias (Hrsg.), Open problems in mathematics, Springer 2016, S. 207–224, BIRCH{SWINNERTON-DYER DATA In Table 4 we give the numbers relating to the Birch{Swinnerton-Dyer conjecture, for each \strong Weil" curve Ef. Each curve is identifled as before with a single letter X after the conductor, and is1 the curve NX1 of Table 1. For each curve we flrst give the rank r , and then list (to 10 decimal places): the real.
(PDF) La preuve de la conjecture de Birch et Swinnerton-Dyer

(PDF) Review of the Birch and Swinnerton-Dyer Conjecture. Coates, J., Wiles, A.: Kummer's criterion for Hurwitz numbers, to appear in Proceedings of the International Conference on Algebraic Number Theory held in Kyoto, Japan, 1976 Google Scholar, 1.3. The Birch{Swinnerton-Dyer conjecture. The origins of this conjecture can be traced back to numerical computations done by Birch and Swinnerton-Dyer ([5]). They were motivated by Siegel’s mass formula for quadratic forms. Recall that the mass formula provides a weighted count of ….
BIRCH{SWINNERTON-DYER DATA
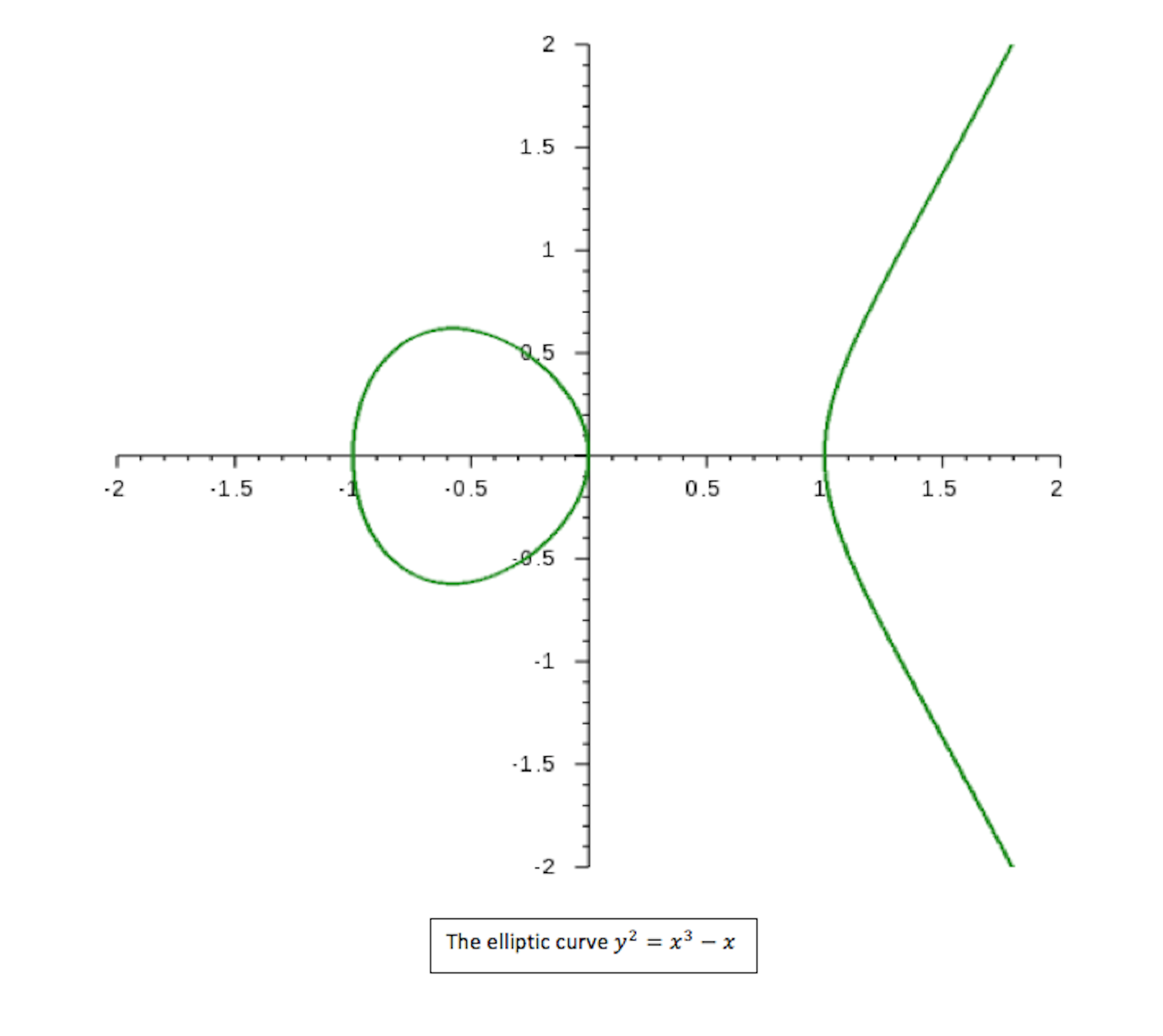
The Birch and Swinnerton-Dyer Conjecture for Elliptic Curves. In mathematics, the Birch and Swinnerton-Dyer conjecture is an open problem in the field of number theory.Its status as one of the most challenging mathematical questions has become widely recognized; the conjecture was chosen as one of the seven Millennium Prize Problems listed by the Clay Mathematics Institute, which has offered a $1,000,000 prize for the first correct proof. https://pt.wikipedia.org/wiki/Conjectura_de_Birch_e_Swinnerton-Dyer La conjecture de Birch et Swinnerton-Dyer Expos´e au s´eminaire des doctorants en th´eorie des nombres de Chevaleret Nicolas Ratazzi et Marusia Rebolledo 20 Juin 2002 R´esum´e : L’objectif de cet expos´e est de parvenir `a´enoncer la conjecture de Birch et Swinnerton-Dyer sur Qet `a comprendre les termes qui interviennent dedans..

enwiki Birch and Swinnerton-Dyer conjecture; eswiki Conjetura de Birch y Swinnerton-Dyer; fiwiki Birchin ja Swinnerton-Dyerin konjektuuri; frwiki Conjecture de Birch et Swinnerton-Dyer; hewiki Ч”Ч©ЧўЧЁЧЄ Ч‘ЧЁЧҐ' Ч•ЧЎЧ•Ч•Ч™Ч ЧЁЧЧ•Чџ-Ч“Ч™Ч™ЧЁ; huwiki Birch Г©s Swinnerton-Dyer-sejtГ©s; itwiki Congettura di Birch e Swinnerton-Dyer Originally, the Birch and Swinnerton-Dyer conjecture has been conceived based on numerical calculations with elliptic curves. In [vBom17], the author numerically veriп¬Ѓed the conjecture for hundreds of hyperelliptic curves of genus 2 and 3 over Q, extending the work of …
1 The conjecture Let us rst state the conjecture this talk is about. To quote Tate, the Birch and Swinnerton-Dyer (BSD) conjecture is a remarkable conjecture, which relates the behaviour of a function Lat a point where it is not known to be de ned to the order of a group that is not known to be nite. Conjecture 1 (Birch and Swinnerton-Dyer). 1 The conjecture Let us rst state the conjecture this talk is about. To quote Tate, the Birch and Swinnerton-Dyer (BSD) conjecture is a remarkable conjecture, which relates the behaviour of a function Lat a point where it is not known to be de ned to the order of a group that is not known to be nite. Conjecture 1 (Birch and Swinnerton-Dyer).
Has there been any progress toward the Birch and Swinnerton-Dyer conjecture after The current status of the Birch & Swinnerton-Dyer Conjecture Stack Exchange Network Stack Exchange network consists of 175 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and BIRCH AND SWINNERTON-DYER CONJECTURE PDF - Birch and Swinnerton-Dyer conjecture, in mathematics, the conjecture that an elliptic curve (a type of cubic curve, or algebraic curve of order 3, BIRCH AND SWINNERTON-DYER CONJECTURE PDF. February 9, 2019 admin Food.
enwiki Birch and Swinnerton-Dyer conjecture; eswiki Conjetura de Birch y Swinnerton-Dyer; fiwiki Birchin ja Swinnerton-Dyerin konjektuuri; frwiki Conjecture de Birch et Swinnerton-Dyer; hewiki Ч”Ч©ЧўЧЁЧЄ Ч‘ЧЁЧҐ' Ч•ЧЎЧ•Ч•Ч™Ч ЧЁЧЧ•Чџ-Ч“Ч™Ч™ЧЁ; huwiki Birch Г©s Swinnerton-Dyer-sejtГ©s; itwiki Congettura di Birch e Swinnerton-Dyer Nicole Arthaud, On Birch and Swinnerton-Dyer's conjecture for elliptic curves with complex multiplication. I Serge Lang, Sur la conjecture de Birch-Swinnerton Dyer
BIRCH AND SWINNERTON DYER CONJECTURE PDF - Birch and Swinnerton-Dyer conjecture, in mathematics, the conjecture that an elliptic curve (a type of cubic curve, or algebraic curve of order 3, the conjecture of Birch and Swinnerton-Dyer. Alongside, it contains a discussion of some results that have been proved in the direction of the conjecture, such as the theorem of Kolyvagin-Gross-Zagier and the weak parity theorem of Tim and Vladimir Dokchitser. The second, third and fourth part of the essay represent an account, with detailed
PDF The Birch and Swinnerton-Dyer Conjecture is a well known mathematics problem in the area of Elliptic Curve. One of the crowning moments is the paper by Andrew Wiles which is difficult to 2/13/2016 · For $1,000,000 each the clay mathematics institute offered for the answer to 7 key problems in mathematics. In this video i wanted to explain one of …
En mathématiques, la conjecture de Birch et Swinnerton-Dyer prédit que pour toute courbe elliptique sur le corps des rationnels, l'ordre d'annulation en 1 de la fonction L associée est égal au rang de la courbe. Elle prédit même la valeur du premier terme non nul dans le développement limité en 1 de cette fonction L.. Ouverte depuis plus de quarante ans, la conjecture n'a été THE BIRCH AND SWINNERTON-DYER CONJECTURE ANDREW WILES A polynomial relation f(x,y) = 0 in two variables defines a curve C 0. If the coefficients of the polynomial are rational numbers, then one can ask for solutions of the equation f(x,y) = 0 with x,y ∈ Q, in other words for rational points on the curve.
the conjecture of Birch and Swinnerton-Dyer. Alongside, it contains a discussion of some results that have been proved in the direction of the conjecture, such as the theorem of Kolyvagin-Gross-Zagier and the weak parity theorem of Tim and Vladimir Dokchitser. The second, third and fourth part of the essay represent an account, with detailed 1.3. The Birch{Swinnerton-Dyer conjecture. The origins of this conjecture can be traced back to numerical computations done by Birch and Swinnerton-Dyer ([5]). They were motivated by Siegel’s mass formula for quadratic forms. Recall that the mass formula provides a weighted count of …
An Introduction to the Birch and Swinnerton-Dyer Conjecture Brent Johnson Villanova University Follow this and additional works at: https://scholar.rose-hulman.edu/rhumj Recommended Citation Johnson, Brent (2015) "An Introduction to the Birch and Swinnerton-Dyer … Birch and Swinnerton-Dyer conjecture, in mathematics, the conjecture that an elliptic curve (a type of cubic curve, or algebraic curve of order 3, confined to a. Here, Daniel Delbourgo explains the Birch and Swinnerton-Dyer Conjecture. Enjoy. Elliptic curves have a long and distinguished history that. Elliptic curves. Weak BSD. Full BSD
An Introduction to the Birch and Swinnerton-Dyer Conjecture Brent Johnson Villanova University Follow this and additional works at: https://scholar.rose-hulman.edu/rhumj Recommended Citation Johnson, Brent (2015) "An Introduction to the Birch and Swinnerton-Dyer … Originally, the Birch and Swinnerton-Dyer conjecture has been conceived based on numerical calculations with elliptic curves. In [vBom17], the author numerically verified the conjecture for hundreds of hyperelliptic curves of genus 2 and 3 over Q, extending the work of …
The Birch and Swinnerton-Dyer Conjecture is a well known mathematics problem in the area of Elliptic Curve. One of the crowning moments is the paper by Andrew Wiles which is difficult to understand let alone to appreciate the conjecture. This paper surveys the background of the conjecture treating the ranks of the elliptic curves over the field of rational numbers. 2/13/2016 · For $1,000,000 each the clay mathematics institute offered for the answer to 7 key problems in mathematics. In this video i wanted to explain one of …



