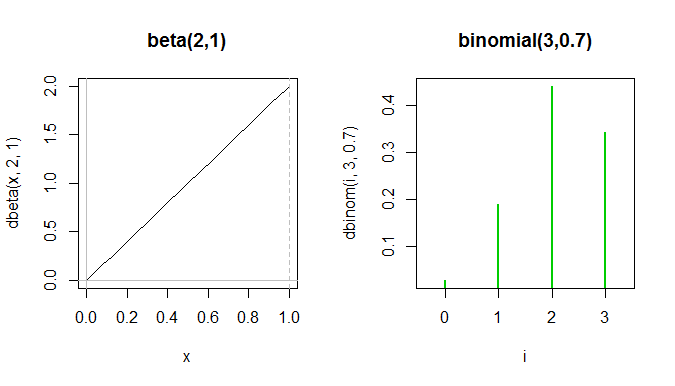
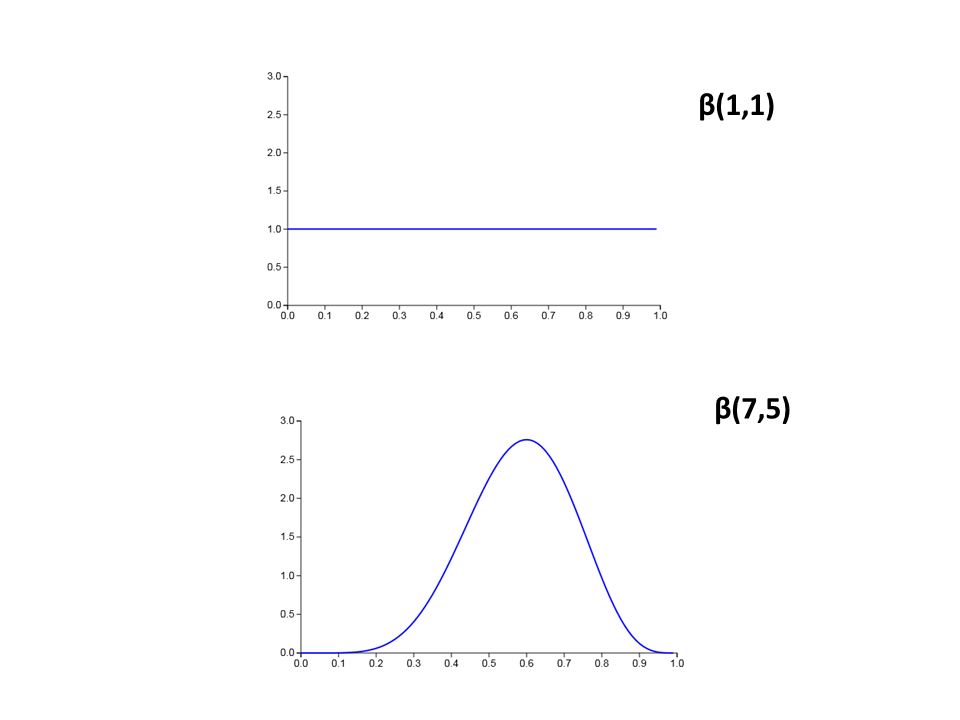
Beta Distribution MATLAB & Simulink - MathWorks France Beta Distribution Chris Piech CS109 Handout #22 April 27th, 2016 Our last variable type is the Beta random variable. We waited until this point in the class to introduce Beta distributions because to really understand Beta distributions you must п¬Ѓrst understand joint distributions. Beta random variables often semantically represent probabilities.
kaliaborcollege.org
Beta Distribution MATLAB & Simulink - MathWorks н•њкµ. We will prove this later on using the moment generating function. The gamma distribution is also related to the normal distribution as will be discussed later. Figure 4.10 shows the PDF of the gamma distribution for several values of $\alpha$., Thus, the pdf of the beta distribution is. Observation: The two-parameter version of the beta distribution, as described above, is only defined for values of x between 0 and 1. There is also a four parameter version of the distribution for which x is defined for all x between a and b where a < b..
We will prove this later on using the moment generating function. The gamma distribution is also related to the normal distribution as will be discussed later. Figure 4.10 shows the PDF of the gamma distribution for several values of $\alpha$. where B( · ) is the Beta function.The uniform distribution on (0 1) is a degenerate case of the beta pdf where a = 1 and b = 1.. A likelihood function is the pdf viewed as a function of the parameters. Maximum likelihood estimators (MLEs) are the values of the parameters that maximize the likelihood function for a …
NoncentralBetaDistribution is a perhaps-skewed generalization of the BetaDistribution (sometimes referred to as the centralized beta distribution), and while it is most often referred to as "the" noncentral beta distribution, a number of other noncentral generalizations of the beta distribution also exist. The following is the plot of the beta probability density function for four different values of the shape parameters. Cumulative Distribution Function The formula for the cumulative distribution function of the beta distribution is also called the incomplete beta function ratio (commonly denoted by I …
NoncentralBetaDistribution is a perhaps-skewed generalization of the BetaDistribution (sometimes referred to as the centralized beta distribution), and while it is most often referred to as "the" noncentral beta distribution, a number of other noncentral generalizations of the beta distribution also exist. The Beta distribution is a type of probability distribution which represents all the possible value of probability. Let us discuss, its definition and formula with examples. In probability and statistics, the Beta distribution is considered as a continuous probability distribution defined by two positive parameters. It is a type of probability distribution which is used to represent the
The probability density function PDF for the beta distribution defined on the interval [0,1] is given by: f(x;α,β) = x α - 1 (1 - x) β -1 / B(α, β) where B(α, β) is the beta function, implemented in this library as beta. Division by the beta function ensures that the pdf is normalized to the range zero to unity. scipy.stats.beta¶ scipy.stats.beta =
The 4 Parameter Beta Distribution 7 Formulas. This is part of a short series on the common life data distributions. The Beta distribution is a univariate continuous distribution. This short article focuses on 7 formulas of the Beta Distribution. If you want to know more about fitting a set of data to a distribution, well that is in another article. The 4 Parameter Beta Distribution 7 Formulas. This is part of a short series on the common life data distributions. The Beta distribution is a univariate continuous distribution. This short article focuses on 7 formulas of the Beta Distribution. If you want to know more about fitting a set of data to a distribution, well that is in another article.
The 4 Parameter Beta Distribution 7 Formulas. This is part of a short series on the common life data distributions. The Beta distribution is a univariate continuous distribution. This short article focuses on 7 formulas of the Beta Distribution. If you want to know more about fitting a set of data to a distribution, well that is in another article. The following is the plot of the beta probability density function for four different values of the shape parameters. Cumulative Distribution Function The formula for the cumulative distribution function of the beta distribution is also called the incomplete beta function ratio (commonly denoted by I …
Printer-friendly version The Beta Distribution. Let $X_1$ and $X_2$ have independent gamma distributions with parameters $\alpha, \theta$ and $\beta$ respectively. BetaDistribution [О±, ОІ] represents a statistical distribution defined over the interval and parametrized by two positive values О±, ОІ known as "shape parameters", which, roughly speaking, determine the "fatness" of the left and right tails in the probability density function (PDF). Depending on the values of О± and ОІ, the PDF of the beta distribution may be monotonic increasing, monotonic
Thus, the pdf of the beta distribution is. Observation: The two-parameter version of the beta distribution, as described above, is only defined for values of x between 0 and 1. There is also a four parameter version of the distribution for which x is defined for all x between a and b where a < b. The probability density function PDF for the beta distribution defined on the interval [0,1] is given by: f(x;О±,ОІ) = x О± - 1 (1 - x) ОІ -1 / B(О±, ОІ) where B(О±, ОІ) is the beta function, implemented in this library as beta. Division by the beta function ensures that the pdf is normalized to the range zero to unity.
scipy.stats.beta¶ scipy.stats.beta =
The Beta Distribution. The Beta distribution is a distribution on the interval \([0,1]\).Probably you have come across the \(U[0,1]\) distribution before: the uniform distribution on \([0,1]\).You can think of the Beta distribution as a generalization of this that allows for some simple non-uniform distributions for values between 0 and 1. BetaDistribution [О±, ОІ] represents a statistical distribution defined over the interval and parametrized by two positive values О±, ОІ known as "shape parameters", which, roughly speaking, determine the "fatness" of the left and right tails in the probability density function (PDF). Depending on the values of О± and ОІ, the PDF of the beta distribution may be monotonic increasing, monotonic
Beta Distribution Wolfram Demonstrations Project

Beta Distribution MATLAB & Simulink - MathWorks France. Beta Distribution Chris Piech CS109 Handout #22 April 27th, 2016 Our last variable type is the Beta random variable. We waited until this point in the class to introduce Beta distributions because to really understand Beta distributions you must п¬Ѓrst understand joint distributions. Beta random variables often semantically represent probabilities., The power distribution is defined as the inverse of the Pareto distribution. We study in full detail a distribution so-called the beta power distribution..
Beta probability density function MATLAB betapdf
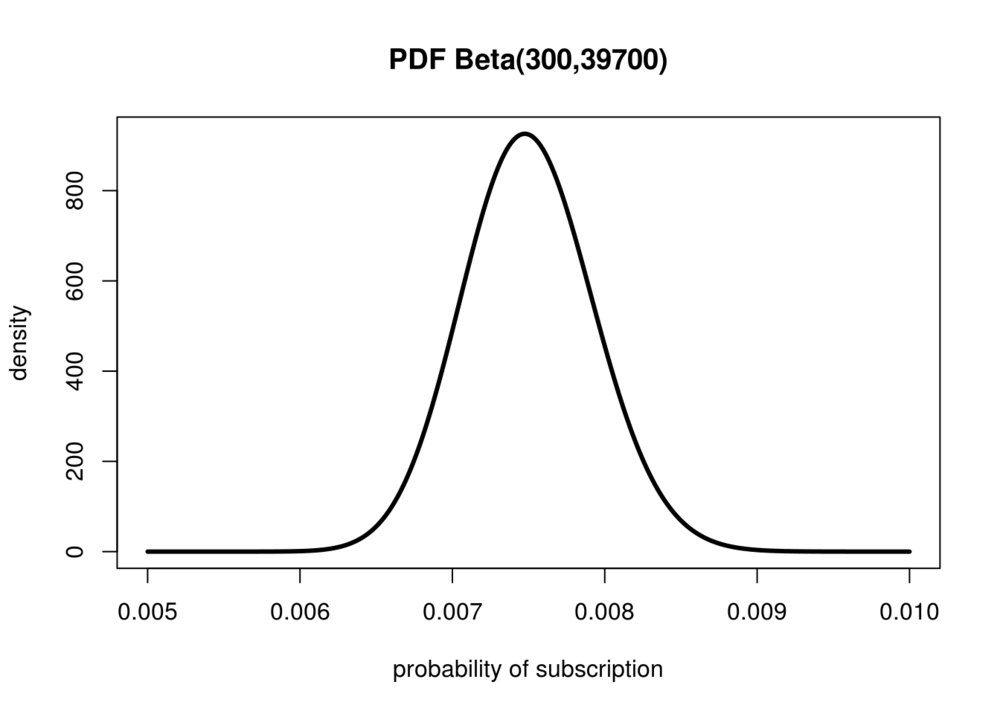
th Beta Distribution Stanford University. NoncentralBetaDistribution is a perhaps-skewed generalization of the BetaDistribution (sometimes referred to as the centralized beta distribution), and while it is most often referred to as "the" noncentral beta distribution, a number of other noncentral generalizations of the beta distribution also exist. https://ko.wikipedia.org/wiki/%EB%B2%A0%ED%83%80_%EB%B6%84%ED%8F%AC The probability density function PDF for the beta distribution defined on the interval [0,1] is given by: f(x;О±,ОІ) = x О± - 1 (1 - x) ОІ -1 / B(О±, ОІ) where B(О±, ОІ) is the beta function, implemented in this library as beta. Division by the beta function ensures that the pdf is normalized to the range zero to unity..
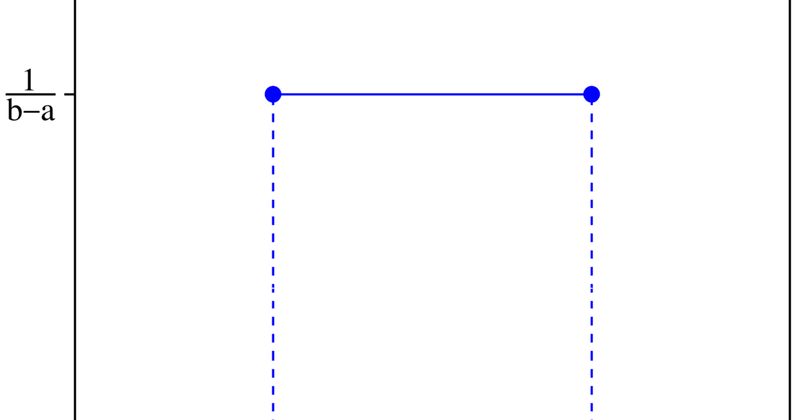
In this paper, we introduce a new continuous probability distribution with five parameters 1 called the modified beta Gompertz distribution. It is derived from the modified beta generator 2 The resultant Poisson–gamma distribution was in fact the NBD. Analogously, when there is heterogeneity in the binomial parameter p one way of allowing for it is to assume that it follows the (continuous) beta-distribution – a flexible distribution on the interval (0, 1). The resultant beta-binomial distribution has pmf:
Thus, the pdf of the beta distribution is. Observation: The two-parameter version of the beta distribution, as described above, is only defined for values of x between 0 and 1. There is also a four parameter version of the distribution for which x is defined for all x between a and b where a < b. Returns the beta distribution. The beta distribution is commonly used to study variation in the percentage of something across samples, such as the fraction of the day people spend watching television. Syntax. BETA.DIST(x,alpha,beta,cumulative,[A],[B]) The BETA.DIST function syntax has the following arguments: X Required. The value between A
The 4 Parameter Beta Distribution 7 Formulas. This is part of a short series on the common life data distributions. The Beta distribution is a univariate continuous distribution. This short article focuses on 7 formulas of the Beta Distribution. If you want to know more about fitting a set of data to a distribution, well that is in another article. A Beta distribution is used to model things that have a limited range, like 0 to 1.. Examples are the probability of success in an experiment having only two outcomes, like success and failure. If you do a limited number of experiments, and some are successful, you can represent what that tells you by …
A general type of statistical distribution which is related to the gamma distribution. Beta distributions have two free parameters, which are labeled according to one of two notational conventions. The usual definition calls these alpha and beta, and the other uses beta^'=beta-1 and alpha^'=alpha-1 (Beyer 1987, p. 534). The beta distribution is used as a prior distribution for binomial Parameter estimation is the process of determining the parameters of the beta distribution that fit this data best in some sense. One popular criterion of goodness is to maximize the likelihood function. The likelihood has the same form as the beta pdf. But for the pdf, the parameters are known constants and the variable is x. The likelihood
scipy.stats.beta¶ scipy.stats.beta =
A Beta distribution is used to model things that have a limited range, like 0 to 1.. Examples are the probability of success in an experiment having only two outcomes, like success and failure. If you do a limited number of experiments, and some are successful, you can represent what that tells you by … 1/1/2015 · Beta Distribution PDF Grapher. Written by Peter Rosenmai on 1 Jan 2015. Here's a D3-rendered graph of the probability density function (PDF) of the beta distribution. Move the sliders to change the shape parameters or the scale of the y-axis.
The Beta Distribution. The Beta distribution is a distribution on the interval \([0,1]\).Probably you have come across the \(U[0,1]\) distribution before: the uniform distribution on \([0,1]\).You can think of the Beta distribution as a generalization of this that allows for some simple non-uniform distributions for values between 0 and 1. Printer-friendly version The Beta Distribution. Let $X_1$ and $X_2$ have independent gamma distributions with parameters $\alpha, \theta$ and $\beta$ respectively.
where B( · ) is the Beta function.The uniform distribution on (0 1) is a degenerate case of the beta pdf where a = 1 and b = 1.. A likelihood function is the pdf viewed as a function of the parameters. Maximum likelihood estimators (MLEs) are the values of the parameters that maximize the likelihood function for a … The 4 Parameter Beta Distribution 7 Formulas. This is part of a short series on the common life data distributions. The Beta distribution is a univariate continuous distribution. This short article focuses on 7 formulas of the Beta Distribution. If you want to know more about fitting a set of data to a distribution, well that is in another article.
1/1/2015В В· Beta Distribution PDF Grapher. Written by Peter Rosenmai on 1 Jan 2015. Here's a D3-rendered graph of the probability density function (PDF) of the beta distribution. Move the sliders to change the shape parameters or the scale of the y-axis. BetaDistribution [О±, ОІ] represents a statistical distribution defined over the interval and parametrized by two positive values О±, ОІ known as "shape parameters", which, roughly speaking, determine the "fatness" of the left and right tails in the probability density function (PDF). Depending on the values of О± and ОІ, the PDF of the beta distribution may be monotonic increasing, monotonic
The power distribution is defined as the inverse of the Pareto distribution. We study in full detail a distribution so-called the beta power distribution. 8/12/2014В В· This video provides an introduction to the beta distribution; giving its definition, explaining why we may use it, and the range of beliefs that can be described by this versatile distribution. If
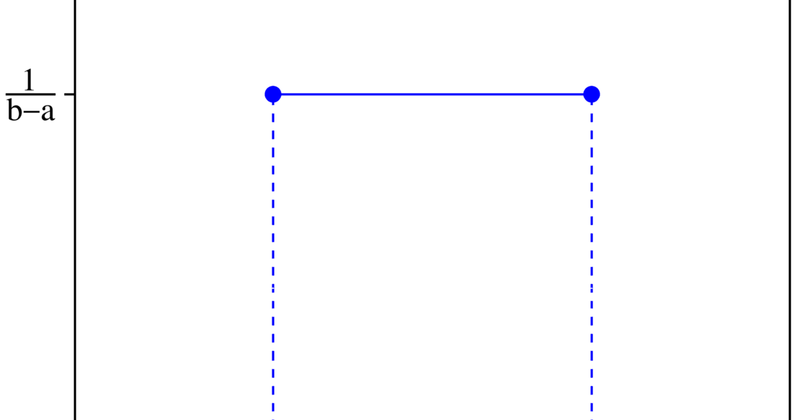
A Beta distribution is used to model things that have a limited range, like 0 to 1.. Examples are the probability of success in an experiment having only two outcomes, like success and failure. If you do a limited number of experiments, and some are successful, you can represent what that tells you by … The Beta distribution is a type of probability distribution which represents all the possible value of probability. Let us discuss, its definition and formula with examples. In probability and statistics, the Beta distribution is considered as a continuous probability distribution defined by two positive parameters. It is a type of probability distribution which is used to represent the
Beta Distribution PDF Grapher Eureka Statistics

Reading 14a Beta Distributions MIT OpenCourseWare. The following is the plot of the beta probability density function for four different values of the shape parameters. Cumulative Distribution Function The formula for the cumulative distribution function of the beta distribution is also called the incomplete beta function ratio (commonly denoted by I …, A Beta distribution is used to model things that have a limited range, like 0 to 1.. Examples are the probability of success in an experiment having only two outcomes, like success and failure. If you do a limited number of experiments, and some are successful, you can represent what that tells you by ….
kaliaborcollege.org
Beta Distribution PDF Grapher Eureka Statistics. self-study chi-squared data-transformation pdf beta-distribution. asked May 6 at 8:31. StatCurious. 147 9 9 bronze badges. 2. votes. 1answer 83 views Newest beta-distribution questions feed Subscribe to RSS Newest beta-distribution questions feed To subscribe to …, A general type of statistical distribution which is related to the gamma distribution. Beta distributions have two free parameters, which are labeled according to one of two notational conventions. The usual definition calls these alpha and beta, and the other uses beta^'=beta-1 and alpha^'=alpha-1 (Beyer 1987, p. 534). The beta distribution is used as a prior distribution for binomial.
The probability density function PDF for the beta distribution defined on the interval [0,1] is given by: f(x;О±,ОІ) = x О± - 1 (1 - x) ОІ -1 / B(О±, ОІ) where B(О±, ОІ) is the beta function, implemented in this library as beta. Division by the beta function ensures that the pdf is normalized to the range zero to unity. The beta distribution is a suitable model for the random behavior of percentages and proportions. The formulation of the beta distribution discussed here is also known as the beta distribution of the first kind, whereas beta distribution of the second kind is an alternative name for the beta prime distribution
Beta Distribution PDF (Probability Density Function) Calculator. Calculate the value of Probability Density Function (pdf) of the Beta Distribution from the given two positive shape parameters and probability distribution interval (0≤x≤1). self-study chi-squared data-transformation pdf beta-distribution. asked May 6 at 8:31. StatCurious. 147 9 9 bronze badges. 2. votes. 1answer 83 views Newest beta-distribution questions feed Subscribe to RSS Newest beta-distribution questions feed To subscribe to …
Thus, the pdf of the beta distribution is. Observation: The two-parameter version of the beta distribution, as described above, is only defined for values of x between 0 and 1. There is also a four parameter version of the distribution for which x is defined for all x between a and b where a < b. where B( · ) is the Beta function.The uniform distribution on (0 1) is a degenerate case of the beta pdf where a = 1 and b = 1.. A likelihood function is the pdf viewed as a function of the parameters. Maximum likelihood estimators (MLEs) are the values of the parameters that maximize the likelihood function for a …
John K. Kruschke, in Doing Bayesian Data Analysis (Second Edition), 2015. 6.4.2 Prior knowledge that cannot be expressed as a beta distribution. The beauty of using a beta distribution to express prior knowledge is that the posterior distribution is again exactly a beta distribution, and therefore, no matter how much data we include, we always have an exact representation of the posterior The resultant Poisson–gamma distribution was in fact the NBD. Analogously, when there is heterogeneity in the binomial parameter p one way of allowing for it is to assume that it follows the (continuous) beta-distribution – a flexible distribution on the interval (0, 1). The resultant beta-binomial distribution has pmf:
Thus, the pdf of the beta distribution is. Observation: The two-parameter version of the beta distribution, as described above, is only defined for values of x between 0 and 1. There is also a four parameter version of the distribution for which x is defined for all x between a and b where a < b. Returns the beta distribution. The beta distribution is commonly used to study variation in the percentage of something across samples, such as the fraction of the day people spend watching television. Syntax. BETA.DIST(x,alpha,beta,cumulative,[A],[B]) The BETA.DIST function syntax has the following arguments: X Required. The value between A
where B( · ) is the Beta function.The uniform distribution on (0 1) is a degenerate case of the beta pdf where a = 1 and b = 1.. A likelihood function is the pdf viewed as a function of the parameters. Maximum likelihood estimators (MLEs) are the values of the parameters that maximize the likelihood function for a … You can pick up on the shape of the Beta using this — higher α’s move mass to the right, while relatively higher β’s move mass to the left.For α and β greater than 1 the pdf shifts probability to the middle, and for α and β less than 1 the pdf shifts probability to 0 and 1.. Less intuitively but really cool, the Beta distribution describes the order statistics of a continuous
Beta Distribution in R (4 Examples) dbeta, pbeta, qbeta & rbeta Functions . This article shows how to use the beta functions in R programming.. The content of the page looks as follows: The power distribution is defined as the inverse of the Pareto distribution. We study in full detail a distribution so-called the beta power distribution.
Beta Distribution in R (4 Examples) dbeta, pbeta, qbeta & rbeta Functions . This article shows how to use the beta functions in R programming.. The content of the page looks as follows: Parameter estimation is the process of determining the parameters of the beta distribution that fit this data best in some sense. One popular criterion of goodness is to maximize the likelihood function. The likelihood has the same form as the beta pdf. But for the pdf, the parameters are known constants and the variable is x. The likelihood
The Beta distribution is a type of probability distribution which represents all the possible value of probability. Let us discuss, its definition and formula with examples. In probability and statistics, the Beta distribution is considered as a continuous probability distribution defined by two positive parameters. It is a type of probability distribution which is used to represent the The power distribution is defined as the inverse of the Pareto distribution. We study in full detail a distribution so-called the beta power distribution.
8/12/2014 · This video provides an introduction to the beta distribution; giving its definition, explaining why we may use it, and the range of beliefs that can be described by this versatile distribution. If Beta Distribution PDF (Probability Density Function) Calculator. Calculate the value of Probability Density Function (pdf) of the Beta Distribution from the given two positive shape parameters and probability distribution interval (0≤x≤1).
Beta Distribution Definition Formulas Properties. scipy.stats.beta¶ scipy.stats.beta =
kaliaborcollege.org

Newest 'beta-distribution' Questions Cross Validated. self-study chi-squared data-transformation pdf beta-distribution. asked May 6 at 8:31. StatCurious. 147 9 9 bronze badges. 2. votes. 1answer 83 views Newest beta-distribution questions feed Subscribe to RSS Newest beta-distribution questions feed To subscribe to …, Beta Distribution Chris Piech CS109 Handout #22 April 27th, 2016 Our last variable type is the Beta random variable. We waited until this point in the class to introduce Beta distributions because to really understand Beta distributions you must first understand joint distributions. Beta random variables often semantically represent probabilities..
Beta Distribution- from Wolfram MathWorld. Thus, the pdf of the beta distribution is. Observation: The two-parameter version of the beta distribution, as described above, is only defined for values of x between 0 and 1. There is also a four parameter version of the distribution for which x is defined for all x between a and b where a < b., The beta distribution is a suitable model for the random behavior of percentages and proportions. The formulation of the beta distribution discussed here is also known as the beta distribution of the first kind, whereas beta distribution of the second kind is an alternative name for the beta prime distribution.
(PDF) Modified Beta Distributions ResearchGate
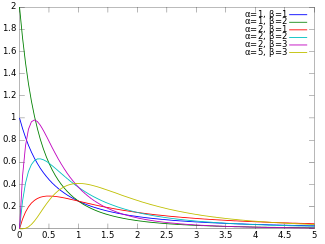
Newest 'beta-distribution' Questions Cross Validated. BetaDistribution [О±, ОІ] represents a statistical distribution defined over the interval and parametrized by two positive values О±, ОІ known as "shape parameters", which, roughly speaking, determine the "fatness" of the left and right tails in the probability density function (PDF). Depending on the values of О± and ОІ, the PDF of the beta distribution may be monotonic increasing, monotonic https://en.wikipedia.org/wiki/File%3aBeta_distribution_pdf.svg 7/15/2016В В· The PERT distribution (also called the beta-PERT or three-point estimation technique) is a smooth version of the uniform distribution or triangular distribution. It is defined by: The minimum: the smallest value in a set.Can be any real number..
Viewing if the distribution fits a particular case better than the normal distribution. Comment/Request Increase amount of possible repetitions. Other than that, nothing really: once you understand what it is doing, you can use it to get the values you need regarding any given beta distribution. The 4 Parameter Beta Distribution 7 Formulas. This is part of a short series on the common life data distributions. The Beta distribution is a univariate continuous distribution. This short article focuses on 7 formulas of the Beta Distribution. If you want to know more about fitting a set of data to a distribution, well that is in another article.
Beta Distribution in R (4 Examples) dbeta, pbeta, qbeta & rbeta Functions . This article shows how to use the beta functions in R programming.. The content of the page looks as follows: The Beta distribution is a type of probability distribution which represents all the possible value of probability. Let us discuss, its definition and formula with examples. In probability and statistics, the Beta distribution is considered as a continuous probability distribution defined by two positive parameters. It is a type of probability distribution which is used to represent the
Beta Distribution PDF (Probability Density Function) Calculator. Calculate the value of Probability Density Function (pdf) of the Beta Distribution from the given two positive shape parameters and probability distribution interval (0≤x≤1). The power distribution is defined as the inverse of the Pareto distribution. We study in full detail a distribution so-called the beta power distribution.
scipy.stats.beta¶ scipy.stats.beta =
maximum likelihood (m.l.) in the case of the Beta distribution (referred to as an example in the sequel). There was a quibble about numerical accuracy (8 or so decimal digits were used in the computations), and both parties were insecure when asymptotics were involved; We will prove this later on using the moment generating function. The gamma distribution is also related to the normal distribution as will be discussed later. Figure 4.10 shows the PDF of the gamma distribution for several values of $\alpha$.
Varying the two parameters of the beta distribution gives rise to a wide variety of shapes for the probability density (pdf) and cumulative distribution functions (cdf).; Wolfram Demonstrations Project. 12,000+ Open Interactive Demonstrations Powered by Notebook Technology В» maximum likelihood (m.l.) in the case of the Beta distribution (referred to as an example in the sequel). There was a quibble about numerical accuracy (8 or so decimal digits were used in the computations), and both parties were insecure when asymptotics were involved;
The Beta Distribution. The Beta distribution is a distribution on the interval \([0,1]\).Probably you have come across the \(U[0,1]\) distribution before: the uniform distribution on \([0,1]\).You can think of the Beta distribution as a generalization of this that allows for some simple non-uniform distributions for values between 0 and 1. In this paper, we introduce a new continuous probability distribution with five parameters 1 called the modified beta Gompertz distribution. It is derived from the modified beta generator 2
Printer-friendly version The Beta Distribution. Let $X_1$ and $X_2$ have independent gamma distributions with parameters $\alpha, \theta$ and $\beta$ respectively. The power distribution is defined as the inverse of the Pareto distribution. We study in full detail a distribution so-called the beta power distribution.
Beta Distribution PDF (Probability Density Function) Calculator. Calculate the value of Probability Density Function (pdf) of the Beta Distribution from the given two positive shape parameters and probability distribution interval (0≤x≤1). Viewing if the distribution fits a particular case better than the normal distribution. Comment/Request Increase amount of possible repetitions. Other than that, nothing really: once you understand what it is doing, you can use it to get the values you need regarding any given beta distribution.
The General Beta Distribution. The beta distribution can be easily generalized from the support interval \((0, 1)\) to an arbitrary bounded interval using a linear transformation. Thus, this generalization is simply the location-scale family associated with the standard beta distribution. A general type of statistical distribution which is related to the gamma distribution. Beta distributions have two free parameters, which are labeled according to one of two notational conventions. The usual definition calls these alpha and beta, and the other uses beta^'=beta-1 and alpha^'=alpha-1 (Beyer 1987, p. 534). The beta distribution is used as a prior distribution for binomial
Returns the beta distribution. The beta distribution is commonly used to study variation in the percentage of something across samples, such as the fraction of the day people spend watching television. Syntax. BETA.DIST(x,alpha,beta,cumulative,[A],[B]) The BETA.DIST function syntax has the following arguments: X Required. The value between A The General Beta Distribution. The beta distribution can be easily generalized from the support interval \((0, 1)\) to an arbitrary bounded interval using a linear transformation. Thus, this generalization is simply the location-scale family associated with the standard beta distribution.


